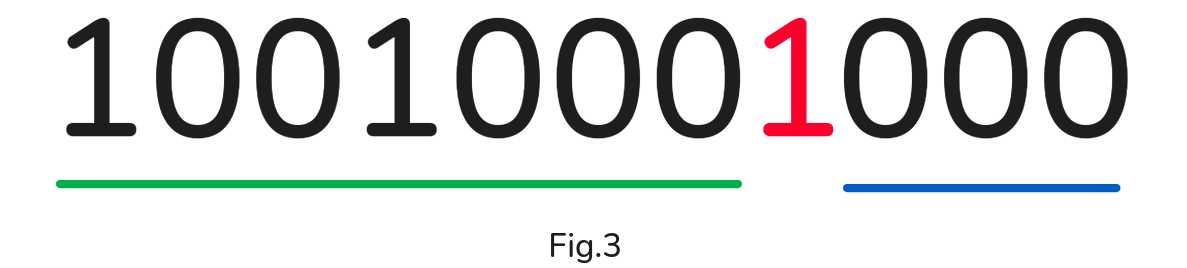Binary Indexed Tree
What is BIT?
A Binary Indexed Tree (BIT), also known as a Fenwick Tree, is essentially an array-based data structure that efficiently handles range queries and updates. It allows you to update values and calculate cumulative sums in O(log_2(n)) time, where n is the size of the array.
How does it store data?
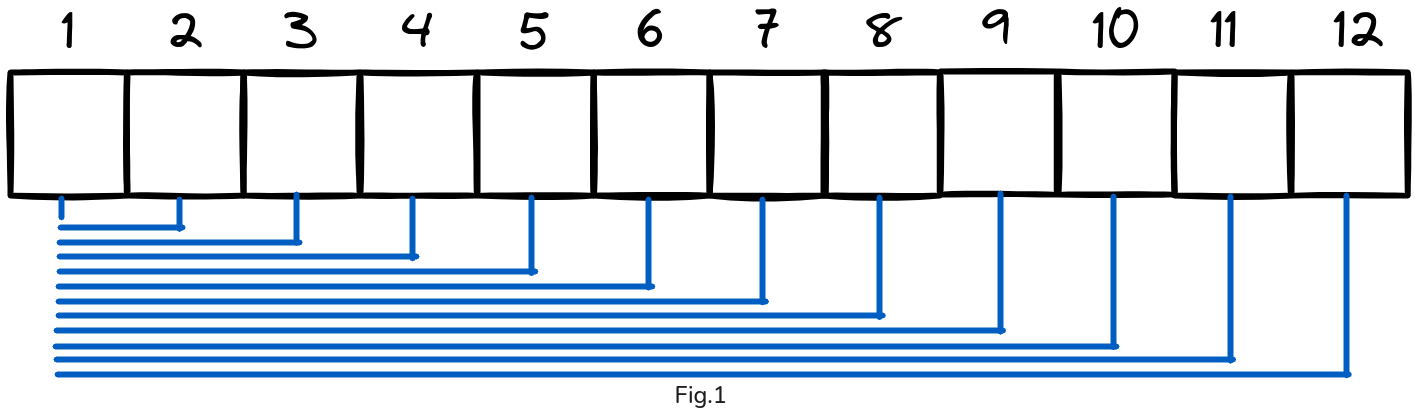
Before exploring the Binary Indexed Tree (BIT), it helps to understand prefix sum array. Given an original array A[1..n], we can precompute its prefix sums in another array P[1..n], where P[i] = A[1] + A[2] + ⋯ + A[i]. (see Fig. 1).
When we increase the value at position idx in A by some amount delta, we must reflect that change in every prefix sum P[j] for all j >= idx.
for j from idx to n:
P[j] := P[j] + deltaThis approach ensures that each P[j] remains the correct sum of the first j elements. However, since each update may touch up to n - idx + 1 entries in P, the worst-case time complexity for a single update is O(n). For large arrays or many updates, this becomes inefficient.
In contrast, a BIT uses a more clever strategy. Instead of storing the complete cumulative sum at every index, each index in a BIT contains the sum of a specific range of elements. The range covered by each index is determined by the value of the least significant bit LSB in its binary representation. This selective storage allows the BIT to query ranges, and update much faster—typically in logarithmic time—compared to a full prefix sum array, where updating a single element requires recalculating all subsequent sums, resulting in linear time complexity.
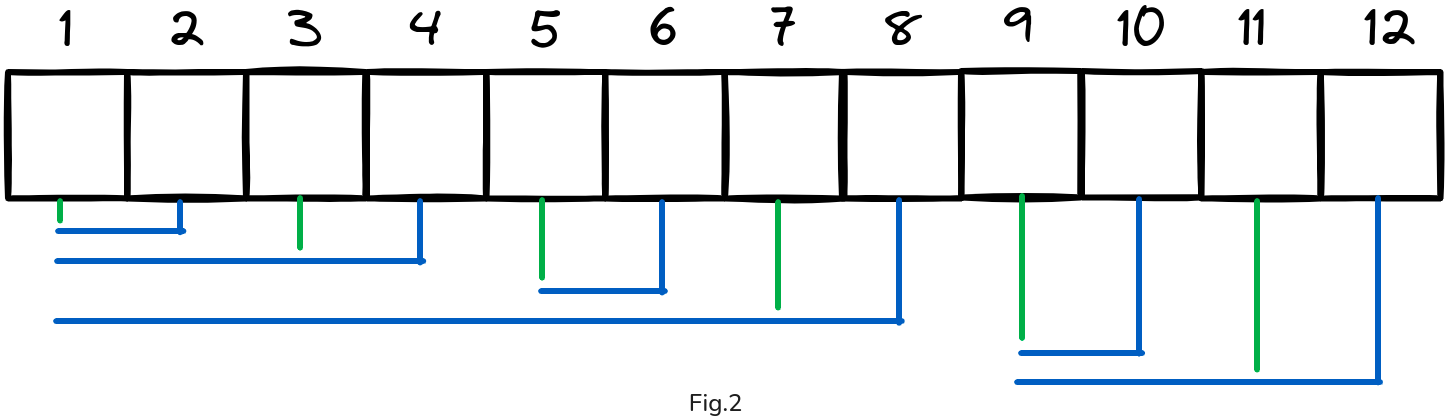
For example, if an index’s LSB is 2 (as in the case of index 6), that BIT entry will contain the sum of the two elements rather than the sum of all elements up to that index (see Fig. 2).
Conclusion
In Figure 1, each index i holds the sum of all elements in the range [1 : i]. By contrast, Figure 2 shows that each index i stores the sum of elements in the range [i−LSB_i+1:i], where LSB_i is the value of the LSB of i in binary. Notice that for odd indices (highlighted in green), where LSB_i equals 1, the index simply stores its own value, as there are no additional elements included in the sum.
BIT Update Function
How to update?
When we want to update a value at index idx, we need to update bit[idx] and also every subsequent BIT position whose stored range includes idx.
For example, if we want to update index 5, then indices 6 and 8 also need to be updated because their ranges cover index 5 (see Fig. 2). Suppose the array is initially filled with zeros, so bit[5], bit[6], and bit[8] are all 0. If we updated the index 5 by 1 (bit[5]:=bit[5]+1), then we must similarly update bit[6] and bit[8], (bit[6]:=bit[6]+1 bit[8]:=bit[8]+1), since they include index 5 in their covered range.
Before diving into how it works in details, let’s define a few key terms:
-
Index
idx- is a pointer referring to the index of the element that should be updated in the original array (not in bit). -
Index
j- is a pointer referring to the next index in the bit whose range contains the indexidx.
Here’s how it works in practice:
First, we update the index idx. Then, we move to the next index j—whose range still covers idx—and update its value. This process is repeated until no further indices need to be updated.
We need a way to move from our current index to the next index j that still includes the index idx in its range. In other words, we must find the smallest j larger than the current index whose coverage extends back to our idx. Clearly, j must be greater than idx—otherwise, it couldn’t include the idx in its range. Thus, the transition from current index to j is done by adding some positive value X to the current index.
Practical example:
Figure 3 shows the binary representation of an example for a idx = 1160.
Before deciding the value of X to add to the current index so the next index still covers index 1160, we need to track two variables:
-
D— the difference betweenjandidx(initially,j = idxsoD = 0). -
LSB_j— initially with theLSBof1160 = 8.
We say that index j covers idx if the number of covered elements by j (the LSB_j) is larger than the difference between j and idx, D < LSB_j.
Note: Initially, idx and j are equal , the LSB_j = 8, D = 0 and D < LSB_j.
There are a limited number of possible options for the addition process, which are listed below. We will prove that only one of them is correct:
-
Xhas bits in the “blue” region:
These bits will increaseD, and decrease theLSB_j, which leads toD >= LSB_j. As a result,jwill never coveridx. So anyXthat sets bits in this region is not an option. -
Xhas bits in the “green” region:
These bits will increaseDwith value greater thanLSB_j, and leave theLSB_junchanged, which leads toD > LSB_j. Consequently,jalso will never coveridx. -
Xhas a bit in the “Red“ region:This bit will increase
Dby theLSB_i, and increase theLSB_jbyLSB_i, So they both are changed by the same value (Dstill less thanLSB_j), and as the current index coversidxthenjwill also coveridx.
Thus, the update function simply adds the LSB of the current index to itself repeatedly to get j, stopping when exceeding array bounds. At each step, we update the BIT value at the new index j.
int lsb(int num){
return num & (-num);
}
void update(int index, int val) {
int i = index;
// While current index is within the bit size, update bit[index].
while (i <= n) {
bit[i] += val; // Update.
i += lsb(i); // Move to the next index.
}
}Time complexity
Each move is executed by adding the LSB_i, which shifts the corresponding bit one position to the left in its binary representation. Given that the number of bits is log_2, the maximum number of moves is log_2, resulting in a time complexity of log_2(n) * t, where t is the time required to update a single bit index.
BIT Query function
How to query?
Unlike a simple prefix sum array where you can obtain the sum for the range ([1, i]) with one operation by accessing P[idx], BIT works differently. Since each index in BIT only holds a portion of the full prefix sum, you need to perform up to log_2(idx) operations to compute the total. Essentially, to calculate the sum from 1 to idx, you first take the value stored at bit[idx] (which represents the sum in the interval [idx - LSB_{idx} + 1 : idx]), then subtract LSB_{idx} from idx to move to the next index, and repeat this process until you reach index 0.
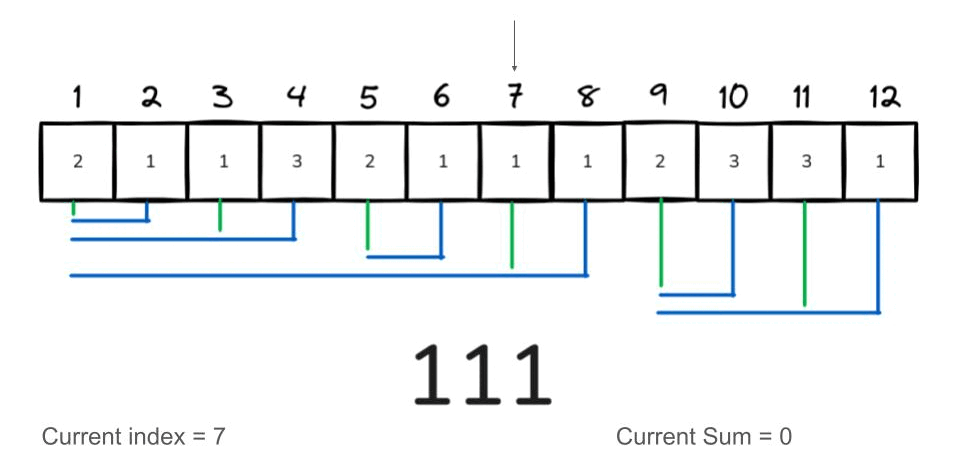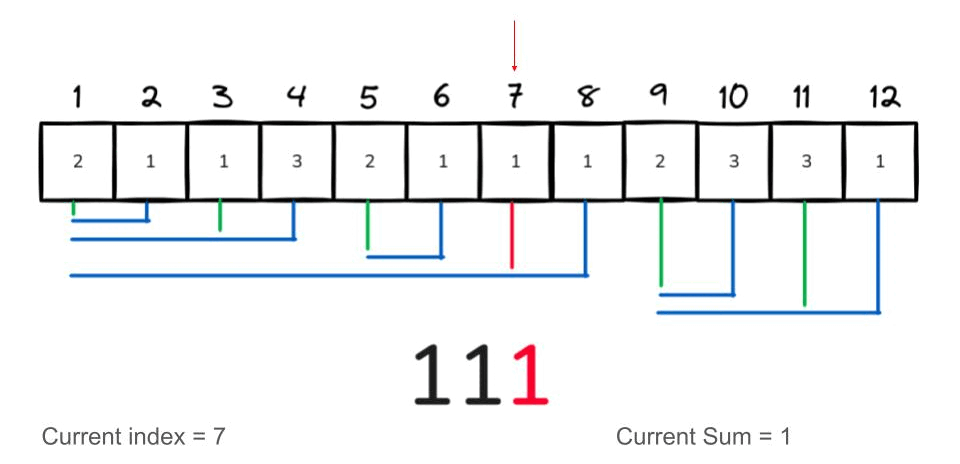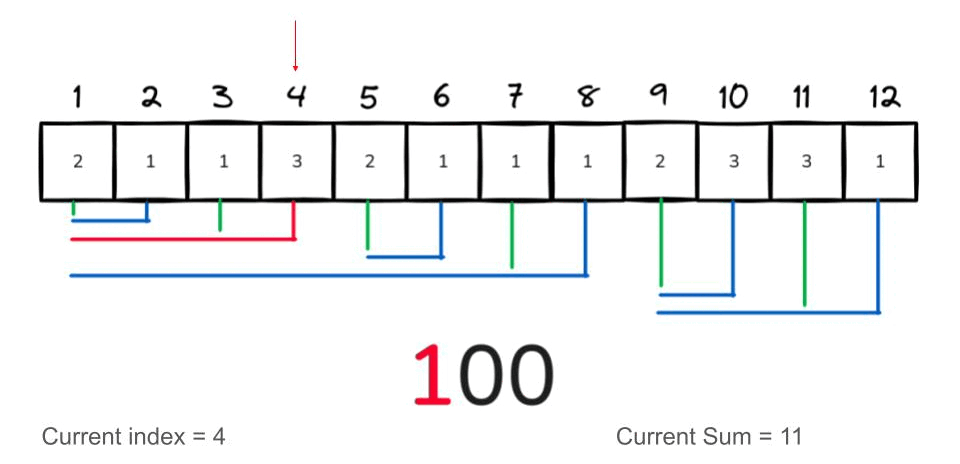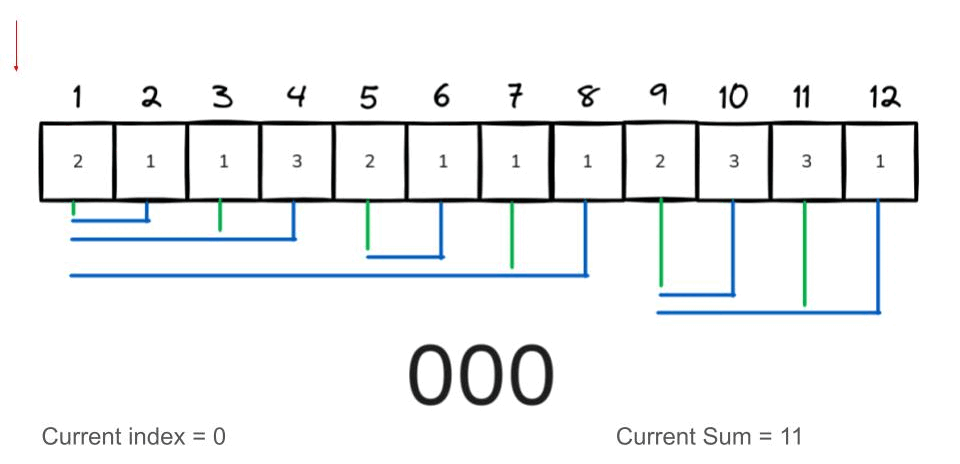
The following GIF demonstrates an example of querying the prefix sum for the range [1:7].
int lsb(int num){
return num & (-num);
}
int query(int index) {
int i = index;
int sum = 0;
while (i > 0) {
sum += bit[i]; // Add the current BIT value to sum.
i -= lsb(i); // Remove the lsb from index.
}
return sum;
}Time complexity
When performing a query, each step removes the LSB from the current index. Since any number can have at most log_2(n) set bits, the query function will execute no more than O(log_2(n)) steps to compute the prefix sum.
BIT Variants
There are some other BIT variants like:
-
Range-Update/Point-Query BIT
-
2D BIT
BIT Template
typedef long long ll;
struct BIT {
vector<ll> bit;
int n;
BIT(int sz, int val = 0) : bit(sz + 2, val), n(sz) {};
int lsb(int num) {
return num & (-num);
}
// Update index 1-based
void update(int index, int val) {
int i = index;
// While current index is within the bit size, update bit[index].
while (i <= n) {
bit[i] += val; // Update.
i += lsb(i); // Move to the next index.
}
}
// get the prefix of the range [1:i]
ll prefix_query(int index) {
int i = index;
ll sum = 0;
while (i > 0) {
sum += bit[i]; // Add the current BIT value to sum.
i -= lsb(i); // Remove the lsb from index.
}
return sum;
}
// get the value of range [l:r]
ll range_query(int l, int r) {
return prefix_query(r) - prefix_query(l - 1);
}
};